Площадь
Содержание
ПоказатьСкрыть
Содержание
Задумывались ли вы, как часто в повседневной жизни мы сталкиваемся с необходимостью рассчитать площадь? Сколько рулонов обоев нужно купить, чтобы обновить стены в квартире? Как не ошибиться с расчетами при покупке ламината для пола? Сколько земли понадобится для посева любимых цветов на даче?

Вопросы простые, но требующие базовых знаний геометрии. Строительство и ремонт, сельское хозяйство, дизайн интерьера и даже кулинария — во всех этих сферах умение рассчитывать площадь становится незаменимым помощником. Будь то раскрой ткани для пошива одежды, вычисление расхода краски для покраски забора или расчет количества плитки для ванной комнаты, умение находить площадь позволяет экономить свое время и деньги, а еще реализовывать идеи максимально эффективно.
И, как ни странно, все эти задачи легко решаются благодаря знанию школьного курса геометрии, а именно — пониманию, что такое площадь фигуры и как ее вычислить.
Итак, давайте вспомним, что же такое площадь фигуры.
Площадь — что это такое
Площадь — это численная характеристика, описывающая размер плоской фигуры. То есть площадь показывает, сколько места занимает фигура на плоскости. В отличие от длины, которая измеряет отрезок, площадь измеряет двумерное пространство.
Понятие площади — это база для решения множества геометрических задач. Она используется для нахождения объемов тел, расчета поверхностей, исследования свойств фигур и, конечно, для применения в практических целях.
Доступ к кредитной истории, бонусам и сервисам — после авторизации
Где применяется?
- Геометрия: вычисление площадей фигур (квадратов, прямоугольников, треугольников, окружностей и т. д.) является одной из основных задач геометрии.
- Исчисление: понятие площади используется для определения интеграла — одной из ключевых концепций матанализа.
- Физика: площадь играет важную роль при расчете давления, силы, работы и других физических величин.
- Инженерия: при проектировании зданий, мостов и других сооружений необходимо учитывать площади различных элементов конструкции.
- Картография: площадь используется для определения размеров стран, регионов и других географических объектов на картах.
Теперь, когда мы освежили в памяти, что такое площадь, давайте разберемся, в каких единицах она измеряется.
Единицы измерения площади
Основные единицы измерения площади:
- Квадратный метр (м²) — наиболее распространенная единица измерения площади в системе СИ. Это площадь квадрата со стороной 1 метр.
- Квадратный сантиметр (см²) — площадь квадрата со стороной 1 сантиметр.
- Квадратный миллиметр (мм²) — площадь квадрата со стороной 1 миллиметр.
- Квадратный километр (км²) — площадь квадрата со стороной 1 километр.
Нестандартные единицы измерения площади:
- Гектар (га) — 10 000 м² (используется в сельском хозяйстве для измерения больших участков земли).
- Ар (а), или сотка, — 100 м² (также используется для измерения земельных участков).
- Квадратный дюйм, квадратный фут, квадратный ярд (используются в некоторых странах, которые не перешли на метрическую систему).
Как сделать перевод между единицами измерения площади?
Важно помнить, что при переводе единиц измерения площади используется соотношение в квадрате. Например:
- 1 м² = 10 000 см² (потому что 1 м = 100 см, значит, 1 м² = 100 см * 100 см = 10 000 см²)
- 1 км² = 1 000 000 м² (потому что 1 км = 1000 м, значит, 1 км² = 1000 м * 1000 м = 1 000 000 м²)
- 1 га = 10 000 м²
Где это важно?
Умение правильно переводить единицы измерения площади необходимо при решении практических задач, например:
- при покупке ткани (если указывать размер в метрах, а считать в сантиметрах, то это может привести к ошибке);
- при планировании строительства (переводить размеры участка из гектаров в квадратные метры для более точных расчетов);
- при сравнении цен на недвижимость (цены могут быть указаны за квадратный метр, а вам нужно знать цену за всю площадь).
Самое время рассмотреть основные формулы для расчета площади геометрических фигур.
Формулы площади фигур: как найти площадь
Ниже разберем, как найти площадь основных геометрических фигур.
Площадь квадрата
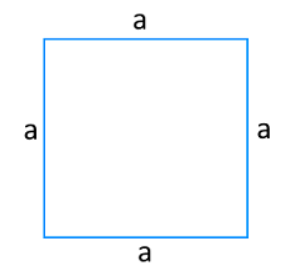
Квадрат — это прямоугольник с равными сторонами. Формула площади квадрата очень проста:
| S = a*a |
где a — длина стороны квадрата.
То есть, чтобы найти площадь квадрата, нужно просто возвести длину его стороны в квадрат.
Например, если сторона квадрата равна 2 см, то его площадь будет равна 2² = 4 см².
Площадь прямоугольника
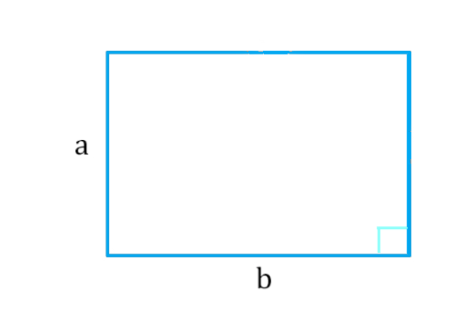
Прямоугольник — это четырехугольник, у которого все углы прямые. Формула площади прямоугольника выглядит так:
| S = a*b |
где a и b — длины сторон прямоугольника. Иными словами, площадь прямоугольника равна произведению длин его сторон.
Например, если длина прямоугольника равна 8 см, а ширина — 3 см, то его площадь будет равна 8 * 3 = 24 см².
Площадь круга
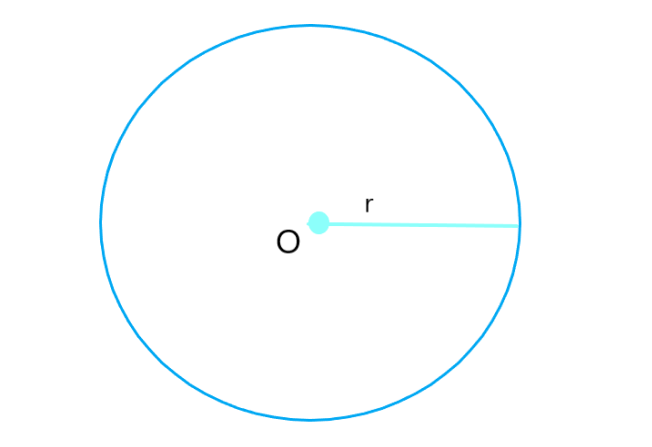
Круг — это геометрическая фигура, состоящая из всех точек плоскости, находящихся на заданном расстоянии (радиусе) от заданной точки (центра круга). Формула площади круга:
| S = π * r² |
где π (пи) — математическая константа, приблизительно равная 3,14159, r — радиус круга. Чтобы найти площадь круга, нужно умножить число π на квадрат радиуса круга.
Например, если радиус круга равен 4 см, то его площадь будет равна π * 4² = 50,27 см².
Площадь треугольника
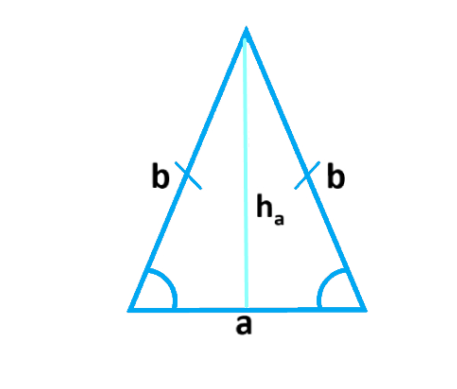
Треугольник — это многоугольник с тремя сторонами и тремя углами. Существует несколько формул площади треугольника в зависимости от известных параметров:
- Через основание и высоту:
| S = (1/2) * a * h |
где a — длина основания треугольника, h — высота, проведенная к этому основанию.
2. Через две стороны и угол между ними:
| S = (1/2) * a * b * sin(γ) |
где a и b — длины двух сторон треугольника, γ — угол между этими сторонами.
3. По формуле Герона (через три стороны):
| S = √(p * (p - a) * (p - b) * (p - c)) |
где a, b, c — длины сторон треугольника, p — полупериметр треугольника
(p = (a + b + c) / 2).
Выбор формулы зависит от того, какие параметры треугольника известны.
Например, если основание треугольника равно 10 см, а высота, проведенная к этому основанию, равна 6 см, то его площадь будет равна (1/2) * 10 * 6 = 30 см².
Площадь трапеции
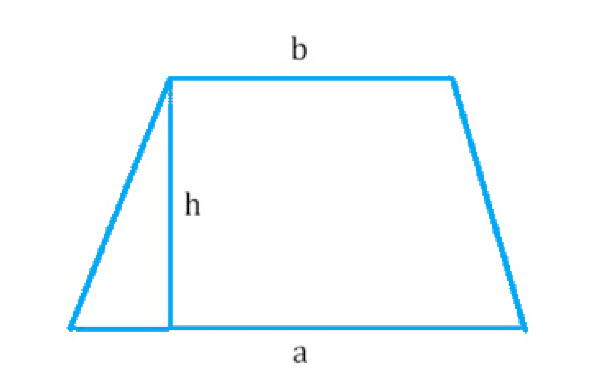
Трапеция — это четырехугольник, у которого две стороны (основания) параллельны, а две другие (боковые) — нет. Формула площади трапеции:
| S = (1/2) * (a + b) * h |
где a и b — длины оснований трапеции, h — высота трапеции (расстояние между основаниями). Чтобы найти площадь трапеции, нужно сложить длины оснований, разделить эту сумму на 2 и умножить на высоту.
Например, если основания трапеции равны 7 см и 5 см, а высота равна 4 см, то ее площадь будет равна (1/2) * (7 + 5) * 4 = 24 см².
Площадь параллелограмма
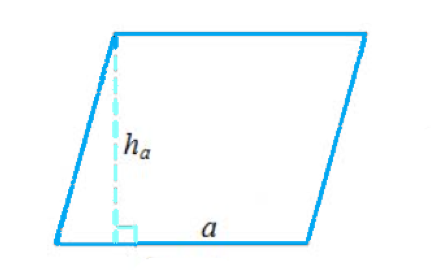
Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны и равны. Формула площади параллелограмма выглядит так:
| S = a * h |
где a — длина стороны параллелограмма, h — высота, проведенная к этой стороне.
Другими словами, площадь параллелограмма равна произведению длины стороны на высоту, проведенную к этой стороне.
Например, если сторона параллелограмма равна 9 см, а высота, проведенная к этой стороне, равна 5 см, то его площадь будет равна 9 * 5 = 45 см².
Площадь ромба
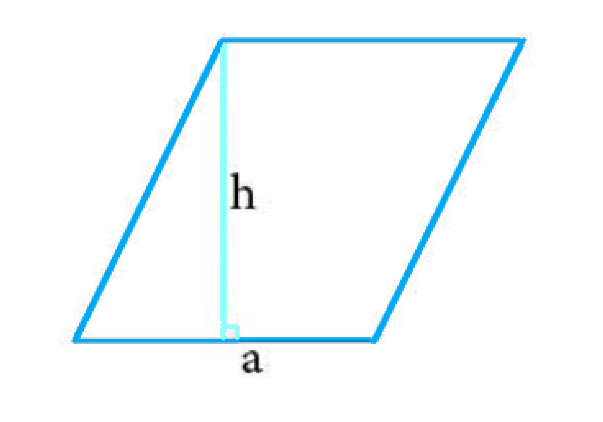
Ромб — это параллелограмм, у которого все стороны равны. Рассмотрим два способа вычисления площади ромба.
- Как параллелограмма:
| S = a * h |
где a — длина стороны ромба, h — высота, проведенная к этой стороне.
2. Через диагонали:
| S = (1/2) * d1 * d2 |
где d1 и d2 — длины диагоналей ромба.
Выбор формулы зависит от того, что известно о ромбе.
Например, если диагонали ромба равны 6 см и 8 см, то его площадь будет равна (1/2) * 6 * 8 = 24 см².
Комментарий эксперта
Понимание концепции площади и умение вычислять ее для различных фигур — это полезный навык, который пригодится как в учебе, так и в повседневной жизни.
Самое важное в изучении площадей — это не просто выучить формулы, а понимать, откуда они берутся. Советую начать с самого простого — с прямоугольника. Представьте, как можно немного изменить прямоугольник, чтобы получить параллелограмм. А если параллелограмм разделить пополам, что получится? Треугольник!
При изучении круга можно представить, как будто он «разворачивается» в треугольник. Основание этого треугольника — длина окружности, а высота — радиус. Это поможет запомнить хитрую формулу πr².
Самое интересное — в расчете площади сложных фигур. В таком случае нужно разбить сложную фигуру на знакомые формы (прямоугольники, треугольники, круги и т. д.), посчитать площадь каждой части, а затем сложить полученные результаты.



