Пришло время подвести итоги конкурса, в котором вы писали посты о банковских продуктах. Спасибо за такое множество полезных, познавательных и содержательных постов!

Знали ли вы, что мошенникам опасно не только называть 4 цифры из смс, но также и последние 4 цифры звонившего номера? Я вот не знала и решила поделиться с вами.
Недели 2 назад стала свидетельницей такой истории. Моей коллеге позвонили якобы из нашего местного пенсионного фонда для уточнения трудового стажа. Для этого ей надо было подойти в пенсионный фонд в определенную дату. Для подтверждения записи на прием коллеге отправили цифровой код, который она им продиктовала. Потом она сразу спохватилась, придумала другой код, но они переспросили - какой код...
Всем привет и самые добрые пожелания. Сегодня 25 февраля.
Захожу в раздел вкладов и вижу эйфорию. Люди радуются ставкам в 16-18-20% годовых. «Банки расщедрились!», «Время зарабатывать!».
Спасибо всем, кто поделился своими присказками про деньги❤️ Получилась просто золотая коллекция, которую жалко прятать в комментариях. Соберу здесь самые яркие цитаты, чтобы они не потерялись.

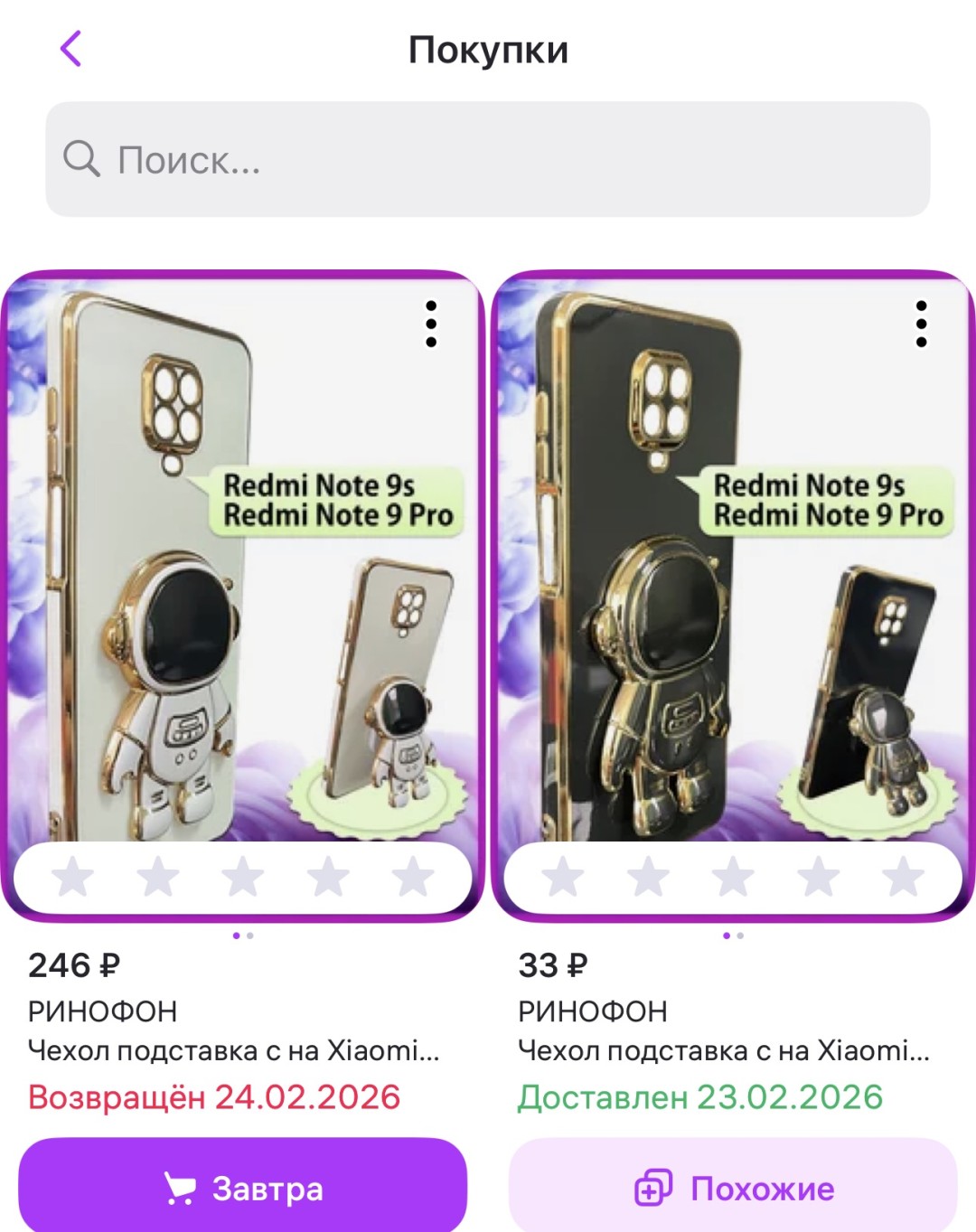
Недавно заказывала на Вайлдберриз чехол на свой телефон, выбрала бюджетную модель. Благополучно забрала заказ домой из пункта выдачи и случайно зашла в карточку товара (обычно так сразу не захожу, лишь изредка сравниваю цены). И что вы думаете? Я купила чехол светлого цвета за 246 рублей, а сейчас появился точно такой же, но черный за 33 рубля. На остатках 1 штука.
Привет! Отгремела Масленица, завершились зимние Олимпийские игры 2026. Наше главное соревнование прошедшей недели — кто съест больше блинов, но даже во время такого сложного челленджа мы не забывали собирать для вас интересные статьи. Предлагаем взглянуть на новый дайджест.

В ноябре я потратила приличную сумму денег на подарок близкому человеку. Потом пришел декабрь, а с ним и новогодние приготовления. Подарки родным и близким, наряд к празднованию, новогодний стол. Потом каникулы - походы в бассейн, в кафе, гуляния. Из-за холодов желание утеплиться и накупить кучу теплого шмотья. Траты на здоровье - комплексное УЗИ, гигиена полости рта, траты на платного педиатра из-за болезни ребенка. 14 февраля, 23 февраля... Вот и скатилась я по своей финансовой лестнице.
Помните, мы обсуждали, почему хороших отзывов всегда меньше?
В Диалоге мы запускаем формат прямого общения с экспертами Банки.ру — возможность задать вопрос и получить ответ от человека, который ежедневно анализирует банки и финансовые продукты.

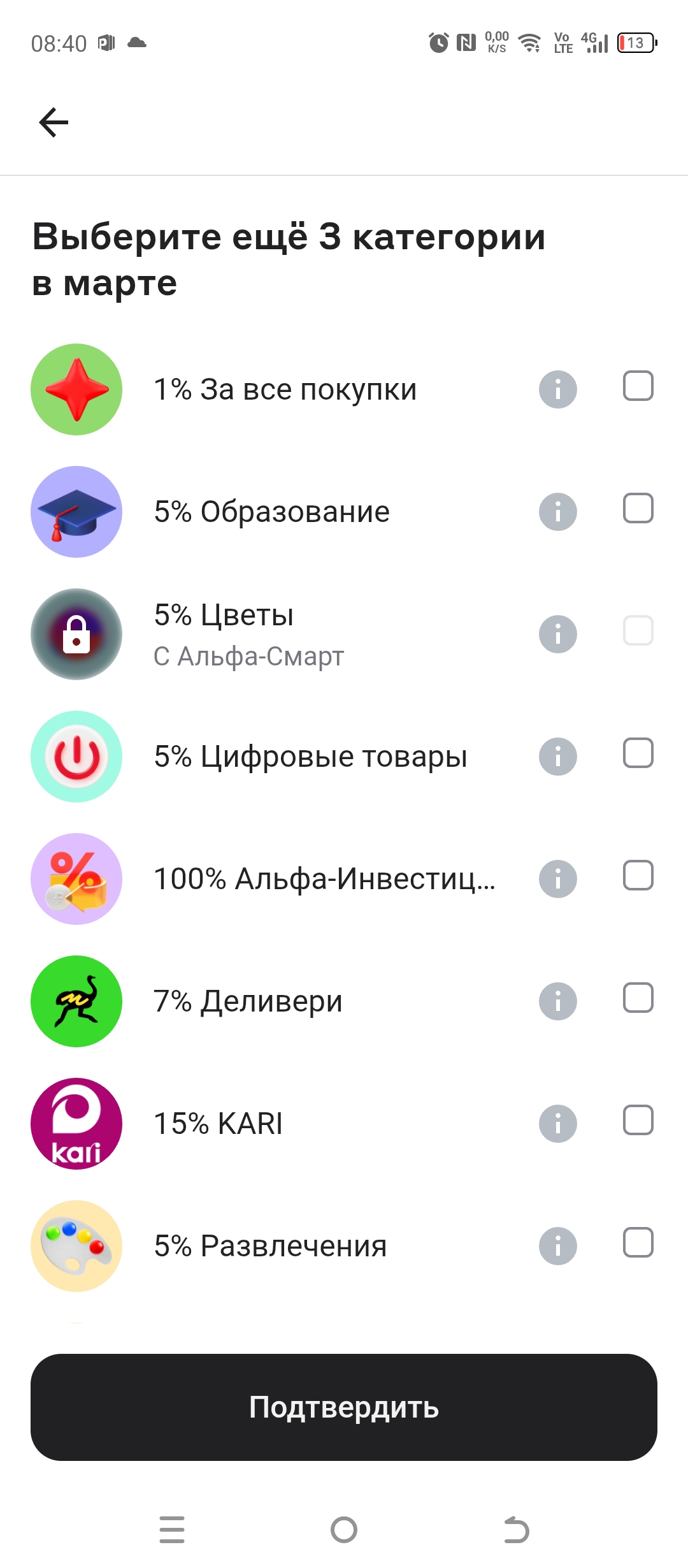
Уже доступны к выбору категории на март от ВТБ. Программа лояльности одного из ведущих банков становится всё более посредственной. Базовый минимум, то есть кэшбэк 5%, нам, видимо, больше не светит.
Вы видели эту красивую анимацию? Крутится барабан, мелькают картинки: вот автомобиль, вот квартира, вот айфоны, куча скидок от разных магазинов. Сотня призов мелькает перед глазами. И мозг автоматически считает: "Раз там около 100 позиций, значит, шанс выиграть машину — примерно 1 к 100. Отличные шансы!"
А вы знали, что у Пятерочки есть свой холодильник, в котором можно вытягивать призы? Найти его не так уж и просто, нужно провалиться в свои баллы и там уже внизу будет плашка с информацией о нём. Поначалу я активно в нём участвовала, но потом забросила это дело. Пару раз выпадали апельсинки, а всё остальное было ненужными купонами от партнеров.
Я тоже заглядываю каждый день в этот холодильник выгоды и призов -- играю в мини-игру и выполняю задания)). Но теперь этот холодильник легче найти - он находится прям под картой Пятёрочки на главной странице приложения (см. скрин). В маленьких корзинах, по сути, ничего интересного нет, а вот большие приносят неплохие баллы.
Сегодня наконец-то появился барабан на продукты в Альфа Банке. Для его появления нужно было объединиться в группу с близкими.
У «Авито» появился конкурент.

С 1 апреля 2026 года для клиентов Premium уровня Bronze лимит бесплатных переводов с кредитной карты снизят на 50 тысяч - до 150 тысяч рублей в месяц. На уровне Silver остается до 200 тысяч, в Privat - до 500 тысяч рублей.
Как пишут «Известия», согласно последним доступным данным Росстата медианная зарплата в России в апреле 2025 года составила 73,4 тыс. рублей. Медиана - это показатель, когда половина получает больше этой суммы, остальные — меньше, а вот по середине будет как раз медиана.
Для всех, кто пользуется онлайн-займами: с 1 марта 2026 года в России вводится обязательная биометрическая идентификация клиентов микрофинансовых организаций (МФО).

На первую покупку в пятницу 27.02.2026. Крутите барабан Альфа- пятницы с 23 до 27 февраля включительно. Чтобы получить кэшбэк до 100%. 27 февраля оплачивайте покупку в приложении или на сайте М. Видео любой картой Альфа-Банка, кроме детской.
При подаче заявки на ипотеку или другой крупный кредит

Привет, банкиры и инвесторы! ЦБ держит ключевую ставку на 18%, и банки конкурируют за ваши рубли. Топ-3 предложения прямо сейчас:Тинькофф Банк: 19,5% на 6 месяцев (мин. 50 000 ₽, онлайн без визита).Сбер: 18,8% на 3 месяца (для новых клиентов, промо до 28.02).ВТБ: 20% на 1 месяц (с пополнением, для зарплатных).Важно: Инфляция ~12%, так что реальная доходность всё равно вкусная. Но проверяйте условия — досрочное снятие убивает процент!Хотите полный рейтинг по 100+ банкам? Загружайте...

Альфа банк предлагает выбрать категории кэшбэка на март , а также крутим барабан кэшбэка.
Информации о последствиях просрочки сегодня более чем достаточно, но многие заемщики все равно нарушают график платежей и избегают общения с взыскателями. Почему так происходит и могут ли современные технологии изменить ситуацию, объясняет генеральный директор ПКО «Защита онлайн» Денис Загребельный.
Вы покупаете товары или услуги, а потом получаете обратно небольшую сумму денег- так работает система кэшбэка — это возврат части потраченных средств обратно на счёт.
Когда я решил проанализировать расходы на банковские услуги, наибольшее удивление вызвали не комиссии за переводы, а стоимость обычных SMS уведомлений. Они списываются незаметно раз в месяц, без каких-либо предупреждений. В моём случае это составило ровно 149 рублей ежемесячно.
Я скорее из тех, кто не читает что написано мелким шрифтом. Я бы точно так не смогла бы.
Ставки по банковским вкладам резко снизились до минимума за последние два года. Сейчас в большинстве банков средние проценты по рублёвым вкладам стали намного ниже, чем раньше: короткие вклады (до 3 месяцев) дают примерно 14–14,2 % годовых, полугодовые — около 13,9 %, а годовые — примерно 12,7–12,8 %
С 1 января 2026 года самозанятые получили право на оплачиваемые больничные. Государство запустило эксперимент, который продлится до 2028 года: плательщики НПД могут добровольно платить взносы и получать выплаты по временной нетрудоспособности. Рассказываем, сколько это стоит и когда выгодно подключаться

Грущу, от того как тают проценты банковских счетов. Вот тихонько и понизился накопительный счет озона, который работает по принципу сейва . Уже 12,5%. А недавно у одного местного автора прочла про втб счет под 15 % и от радости перевела туда свои накопления.