Формулы скорости, времени и расстояния

Задачи на движение могут показаться отголоском школьной программы, однако они имеют прямое отношение к повседневной жизни. Они пригодятся и при планировании поездки на дачу, и при расчете времени прибытия курьера. Понимание взаимосвязи между скоростью, временем и расстоянием помогает эффективно управлять своим временем и ресурсами. Разбираемся в деталях.

Расстояние

Расстояние — это протяженность пути между двумя объектами, выраженная численно. В математике это длина линии между двумя точками в пространстве. Измеряется расстояние в единицах длины: метрах (м), километрах (км), сантиметрах (см) и других.

В повседневной жизни мы постоянно сталкиваемся с расстояниями: от дома до работы, от одного города до другого. Например, расстояние между Москвой и Санкт-Петербургом составляет от 650 км до 720 км в зависимости от маршрута.

В математике расстояние обозначается латинской буквой s и вычисляется по формуле:

s=v×t

где v — скорость, t — время.

Как найти путь по скорости и времени:

• Умножьте скорость на время движения.
• Убедитесь, что единицы измерения согласованы (если скорость в км/ч, то время должно быть в часах).

Простой пример: автомобиль едет со скоростью 60 км/ч в течение 2 часов. Пройденное расстояние: s = 60 × 2 = 120 км.

Формула работает для любых видов движения: пешехода, автомобиля, поезда или самолета. Главное — правильно подставить значения скорости и времени в одинаковых единицах измерения.

Время

Время — это продолжительность событий, выраженная численно. В математических задачах время показывает, как долго происходит движение от начальной до конечной точки. Измеряется в секундах (с), минутах (мин), часах (ч), сутках.

Время в формулах обозначается латинской буквой t. Его через отношение расстояния к скорости:

t=s/v

Как вычислить время при известных скорости и пути:

• Разделите расстояние на скорость.
• Проверьте соответствие единиц измерения.
• Результат покажет продолжительность движения.

Практические примеры:

1. Пешеход и школа: ученик проходит 130 метров от школы до бассейна за 2 минуты. Его скорость составляет 65 м/мин.
2. Поездка на дачу: родители проезжают расстояние от дома до дачи за 3 часа на автомобиле.
3. Расчет времени в пути. Если нужно проехать 180 км со скоростью 60 км/ч, время составит: t = 180 ÷ 60 = 3 часа.

Понимание времени как величины помогает планировать поездки, рассчитывать опоздания и решать множество бытовых задач. В математических задачах время часто становится ключом к нахождению других неизвестных параметров движения.

Скорость

Скорость — это расстояние, которое объект преодолевает за единицу времени. Математически скорость представляет отношение пройденного пути ко времени движения. Измеряется в составных единицах: метрах в секунду (м/с), километрах в час (км/ч), метрах в минуту (м/мин).

Скорость обозначается латинской буквой v и рассчитывается по формуле:

v=s/t

Как рассчитать скорость по расстоянию и времени:

• Разделите пройденное расстояние на затраченное время.
• Убедитесь в правильности единиц измерения.
• Результат покажет среднюю скорость движения.

Практические примеры:

• Ученик идет со скоростью 65 м/мин.
• Автомобиль движется со скоростью 60 км/ч.
• При прохождении 240 км за 4 часа скорость составит: v = 240 /4 = 60 км/ч.

Примеры решения задач

Задача 1 (легкий уровень): Турист шел со скоростью 5 км/ч в течение 2 часов 12 минут. Найти расстояние.

Решение: s = v × t = 5 × (2 + 12/60) = 5 × 2,2 = 11 км.

Задача 2 (средний уровень): Электровелосипед проехал 5,4 км со скоростью 1,5 м/с. Найти время в пути.

Решение: t = s / v = 5400 м / 1,5 м/с = 3600 с = 1 час.

Задача 3 (сложный уровень): Лодка прошла по течению 24 км за 2 ч и против течения 18 км за 3 ч. Найти собственную скорость лодки в стоячей воде.

Решение: vлод = (s↓/t↓ + s↑/t↑) / 2 = (12 + 6) / 2 = 9 км/ч.

Взаимосвязь скорости, времени и расстояния

Три основные величины движения находятся в строгой математической зависимости. Эта связь описывается треугольником формул, где каждый параметр можно найти через два других.

Базовая формула связи:

s=v×t

Из нее выводятся остальные:

v=s/t  (скорость равна расстоянию, деленному на время) и t=s/v (время равно расстоянию, деленному на скорость).

Эту формулу и две ее производные легко запомнить с помощью «магического треугольника». Для этого нужно представить треугольник, разделенный на три части. Наверху находится S (расстояние), а внизу, рядом друг с другом, — V (скорость) и t (время). Чтобы найти нужную величину, достаточно мысленно прикрыть ее пальцем.

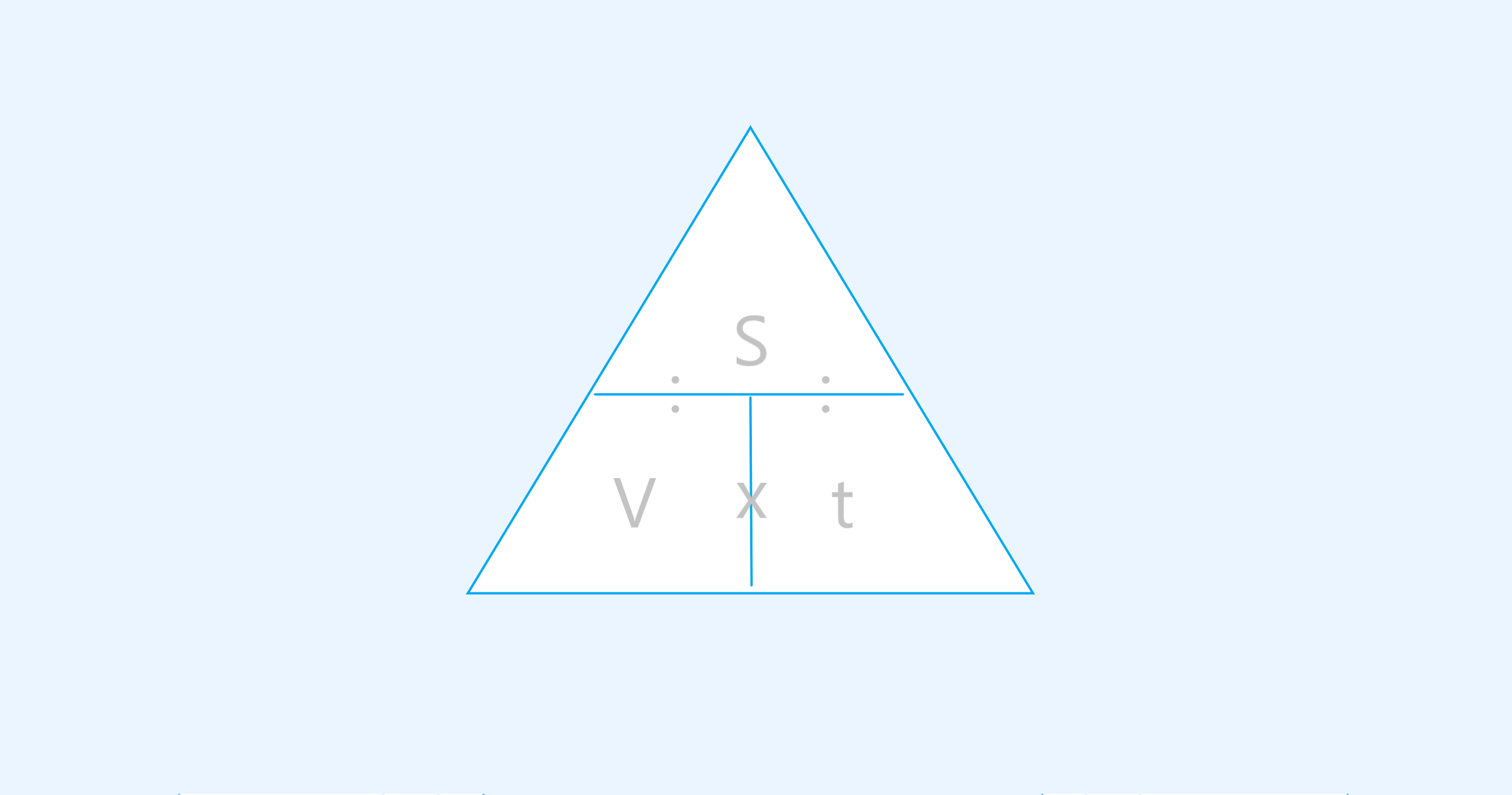
Прикрыв S, вы увидите V и t рядом, что означает умножение. Прикрыв V, вы увидите S над t, что означает деление. Прикрыв t, вы увидите S над  V, что также означает деление.

Эта взаимосвязь работает для любых видов равномерного движения и составляет основу решения задач на движение в математике и физике. Понимание этих зависимостей помогает в повседневной жизни: например, при планировании поездок, расчете времени в пути, определении оптимальной скорости движения.